付録 2: バイナリヒープ
¶ 第7章では、最小の要素を迅速に見つける方法としてバイナリヒープが紹介されました。約束どおり、この付録ではこのデータ構造の背後にある詳細を説明します。
¶ 改めて、私たちが解決する必要があった問題を考えてみましょう。A*アルゴリズムは大量の小さなオブジェクトを作成し、それらを「オープンリスト」に保持する必要がありました。また、このリストから最小の要素を常に削除していました。最も単純なアプローチは、すべてのオブジェクトを配列に保持し、必要なときに最小のオブジェクトを検索することです。しかし、多くの時間を費やすことができない限り、これはうまくいきません。ソートされていない配列で最小の要素を見つけるには、配列全体を調べて各要素をチェックする必要があります。
¶ 次の解決策は、もちろん、配列をソートすることです。JavaScriptの配列には素晴らしいsortメソッドがあり、これを使用して重い作業を行うことができます。残念ながら、要素が追加されるたびに配列全体を再ソートすることは、ソートされていない配列で最小値を検索するよりも多くの作業が必要です。全体を再ソートする代わりに、新しい値が正しい位置に挿入されるようにして、以前にソートされていた配列がソートされた状態を維持するというようなトリックを使用できます。これはバイナリヒープがすでに使用しているアプローチに近づいていますが、配列の中央に値を挿入するには、それ以降のすべての要素を1つ上に移動する必要があり、それでも遅すぎます。
¶ 別のアプローチとして、配列をまったく使用せず、相互に接続されたオブジェクトの集合に値を格納する方法があります。これの単純な形式は、各オブジェクトに1つの値と、他のオブジェクトへの2つ(またはそれ以下)のリンクを持たせることです。最小の値を持つ1つのルートオブジェクトがあり、これを使用して他のすべてのオブジェクトにアクセスします。リンクは常に値が大きいオブジェクトを指しているので、全体的な構造は次のようになります。
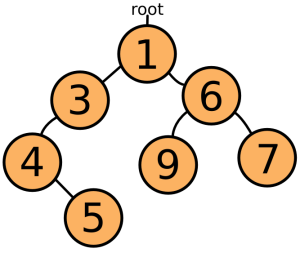
¶ このような構造は、分岐方法からツリーと呼ばれます。最小の要素が必要な場合は、トップの要素を取り除き、トップ要素の子の1つ(値が最も低いもの)が新しいトップになるようにツリーを再配置します。新しい要素を挿入する際には、新しい要素よりも小さい要素が見つかるまでツリーを「下降」し、そこに挿入します。これはソートされた配列よりもはるかに少ない検索で済みますが、多くのオブジェクトが作成されるという欠点があり、これも処理速度を低下させます。
¶ したがって、バイナリヒープはソートされた配列を使用しますが、上記のツリーのように部分的にしかソートされていません。オブジェクトの代わりに、配列の位置を使用してツリーを形成します。この図はそれを示そうとしています。
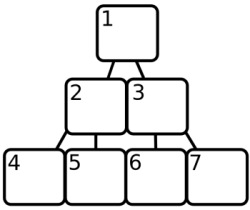
¶ 配列要素1はツリーのルートであり、配列要素2と3はその子であり、一般的に配列要素Xの子はX * 2とX * 2 + 1です。この構造が「ヒープ」と呼ばれる理由がわかります。この配列は1から始まり、JavaScriptの配列は0から始まることに注意してください。ヒープは常に最小の要素を位置1に保持し、配列の位置Xにあるすべての要素について、位置X / 2(切り捨て)にある要素が小さくなるようにします。
¶ 最小の要素を見つけるには、位置1の要素を取得すればよくなりました。しかし、この要素が削除されると、ヒープは配列に穴が残らないようにする必要があります。これを行うには、配列の最後の要素を取得して先頭に移動し、次に位置2と3の子要素と比較します。おそらく大きくなるため、それらのいずれかと交換され、その新しい位置について子要素との比較プロセスが繰り返され、子要素が大きくなる位置、または子が存在しない位置に達するまで続きます。
[2, 3, 5, 4, 8, 7, 6] Take out 2, move 6 to the front. [6, 3, 5, 4, 8, 7] 6 is greater than its first child 3, so swap them. [3, 6, 5, 4, 8, 7] Now 6 has children 4 and 8 (position 4 and 5). It is greater than 4, so we swap again. [3, 4, 5, 6, 8, 7] 6 is in position 4, and has no more children. The heap is in order again.
¶ 同様に、要素をヒープに追加する必要がある場合、配列の最後に配置され、「バブルアップ」して親と繰り返し交換することで、新しいノードよりも小さい親が見つかるまで上昇します。
[3, 4, 5, 6, 8, 7] Element 2 gets added again, it starts at the back. [3, 4, 5, 6, 8, 7, 2] 2 is in position 7, its parent is at 3, which is a 5. 5 is greater than 2, so we swap. [3, 4, 2, 6, 8, 7, 5] The parent of position 3 is position 1. Again, we swap. [2, 4, 3, 6, 8, 7, 5] The element can not go further than position 1, so we are done.
¶ 要素の追加または挿入で、配列のすべての要素と比較する必要がないことに注意してください。実際、親と子の間のジャンプは配列が大きくなるにつれて大きくなるため、要素が多いほどこの利点は特に大きくなります1。
¶ バイナリヒープの実装の完全なコードを次に示します。注目すべき2つの点は、ヒープに配置された要素を直接比較する代わりに、最初に関数(scoreFunction)を適用するため、直接比較できないオブジェクトを格納できることです。
¶ また、JavaScriptの配列は0から始まり、親/子の計算は1から始まるシステムを使用しているため、補正するためのいくつかの奇妙な計算があります。
function BinaryHeap(scoreFunction){ this.content = []; this.scoreFunction = scoreFunction; } BinaryHeap.prototype = { push: function(element) { // Add the new element to the end of the array. this.content.push(element); // Allow it to bubble up. this.bubbleUp(this.content.length - 1); }, pop: function() { // Store the first element so we can return it later. var result = this.content[0]; // Get the element at the end of the array. var end = this.content.pop(); // If there are any elements left, put the end element at the // start, and let it sink down. if (this.content.length > 0) { this.content[0] = end; this.sinkDown(0); } return result; }, remove: function(node) { var length = this.content.length; // To remove a value, we must search through the array to find // it. for (var i = 0; i < length; i++) { if (this.content[i] != node) continue; // When it is found, the process seen in 'pop' is repeated // to fill up the hole. var end = this.content.pop(); // If the element we popped was the one we needed to remove, // we're done. if (i == length - 1) break; // Otherwise, we replace the removed element with the popped // one, and allow it to float up or sink down as appropriate. this.content[i] = end; this.bubbleUp(i); this.sinkDown(i); break; } }, size: function() { return this.content.length; }, bubbleUp: function(n) { // Fetch the element that has to be moved. var element = this.content[n], score = this.scoreFunction(element); // When at 0, an element can not go up any further. while (n > 0) { // Compute the parent element's index, and fetch it. var parentN = Math.floor((n + 1) / 2) - 1, parent = this.content[parentN]; // If the parent has a lesser score, things are in order and we // are done. if (score >= this.scoreFunction(parent)) break; // Otherwise, swap the parent with the current element and // continue. this.content[parentN] = element; this.content[n] = parent; n = parentN; } }, sinkDown: function(n) { // Look up the target element and its score. var length = this.content.length, element = this.content[n], elemScore = this.scoreFunction(element); while(true) { // Compute the indices of the child elements. var child2N = (n + 1) * 2, child1N = child2N - 1; // This is used to store the new position of the element, // if any. var swap = null; // If the first child exists (is inside the array)... if (child1N < length) { // Look it up and compute its score. var child1 = this.content[child1N], child1Score = this.scoreFunction(child1); // If the score is less than our element's, we need to swap. if (child1Score < elemScore) swap = child1N; } // Do the same checks for the other child. if (child2N < length) { var child2 = this.content[child2N], child2Score = this.scoreFunction(child2); if (child2Score < (swap == null ? elemScore : child1Score)) swap = child2N; } // No need to swap further, we are done. if (swap == null) break; // Otherwise, swap and continue. this.content[n] = this.content[swap]; this.content[swap] = element; n = swap; } } };
¶ そして簡単なテスト…
var heap = new BinaryHeap(function(x){return x;}); forEach([10, 3, 4, 8, 2, 9, 7, 1, 2, 6, 5], method(heap, "push")); heap.remove(2); while (heap.size() > 0) print(heap.pop());