第7章: 探索
¶ この章では、JavaScript特有の新しい概念は紹介しません。代わりに、2つの問題の解決策を順を追って説明し、その過程で興味深いアルゴリズムとテクニックについて議論します。興味がなければ、次の章に進んでください。
¶ 最初の問題を紹介します。この地図を見てください。太平洋の小さな熱帯の島、ヒバオアを示しています。
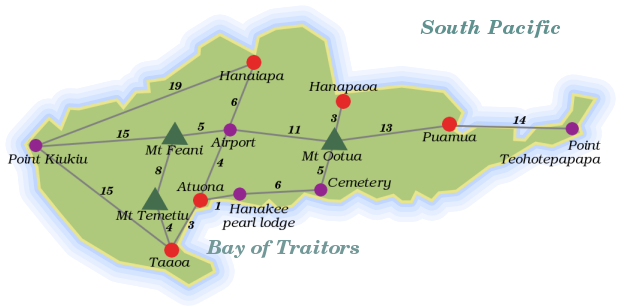
¶ 灰色の線は道路で、その横の数字は道路の長さです。ヒバオアの2点間の最短ルートを見つけるプログラムが必要だと想像してみてください。どのようにアプローチすればよいでしょうか?少し考えてみてください。
¶ いいえ、本当に。次の段落にただ読み進めないでください。真剣にいくつかの方法を考えて、直面するであろう問題を検討してみてください。技術書を読むときは、ただ文章を流し読み、厳粛にうなずき、読んだ内容をすぐに忘れてしまうのは簡単すぎます。問題を解決しようと真剣に努力すれば、それは*あなた*の問題となり、その解決策はより意味のあるものになります。
¶ この問題の最初の側面は、やはりデータの表現です。画像の情報は、コンピュータにはあまり意味がありません。地図を見て情報を抽出するプログラムを書くこともできますが…それは複雑になる可能性があります。解釈する地図が2万枚ある場合は、これは良い考えですが、この場合は自分で解釈を行い、地図をよりコンピュータに適した形式に書き写します。
¶ プログラムは何を知る必要があるでしょうか?どの場所が接続されているか、そしてそれらの間の道路の長さを調べることができる必要があります。島にある場所と道路は、数学者が呼ぶところのグラフを形成しています。グラフを格納する方法はたくさんあります。単純な可能性は、道路オブジェクトの配列を格納することです。各オブジェクトには、2つの端点とその長さを示すプロパティが含まれています…
var roads = [{point1: "Point Kiukiu", point2: "Hanaiapa", length: 19}, {point1: "Point Kiukiu", point2: "Mt Feani", length: 15} /* and so on */];
¶ しかし、プログラムはルートを計算する際に、交差点に立っている人が標識を見て「ハナイヤパ:19km、マウントフェアニ:15km」と読むように、特定の場所から始まるすべての道路のリストを頻繁に取得する必要があることがわかります。これが簡単(そして迅速)にできればいいのですが。
¶ 上記の表現では、この標識リストが必要になるたびに、道路のリスト全体をふるいにかけ、関連するものを選び出す必要があります。より良いアプローチは、このリストを直接格納することです。たとえば、地名と標識リストを関連付けるオブジェクトを使用します
var roads = {"Point Kiukiu": [{to: "Hanaiapa", distance: 19}, {to: "Mt Feani", distance: 15}, {to: "Taaoa", distance: 15}], "Taaoa": [/* et cetera */]};
¶ このオブジェクトがあれば、ポイントキウキウから出ている道路を取得するには、`roads["Point Kiukiu"]`を見るだけで済みます。
¶ ただし、この新しい表現には重複する情報が含まれています。AとBの間の道路は、AとBの両方にリストされています。最初の表現はすでに入力するのに多くの作業が必要でしたが、これはさらに悪いです。
¶ 幸いなことに、私たちはコンピュータの反復作業の才能を自由に使うことができます。道路を一度指定し、正しいデータ構造をコンピュータによって生成させることができます。まず、`roads`という空のオブジェクトを初期化し、`makeRoad`という関数を記述します
var roads = {}; function makeRoad(from, to, length) { function addRoad(from, to) { if (!(from in roads)) roads[from] = []; roads[from].push({to: to, distance: length}); } addRoad(from, to); addRoad(to, from); }
¶ いいですね?内部関数`addRoad`が、外部関数と同じ名前(`from`、`to`)をパラメータに使用していることに注目してください。これらは干渉しません。`addRoad`内では`addRoad`のパラメータを参照し、`addRoad`外では`makeRoad`のパラメータを参照します。
¶ `addRoad`の`if`文は、`from`で指定された場所に対応付けられた宛先配列がまだない場合、空の配列を配置するようにします。こうすることで、次の行はそのような配列があると仮定し、新しい道路を安全にプッシュできます。
¶ これで、地図情報は次のようになります
makeRoad("Point Kiukiu", "Hanaiapa", 19); makeRoad("Point Kiukiu", "Mt Feani", 15); makeRoad("Point Kiukiu", "Taaoa", 15); // ...
¶ 上記の記述では、文字列`"Point Kiukiu"`はまだ3回連続で出現しています。複数の道路を1行で指定できるようにすることで、記述をさらに簡潔にすることができます。
¶ 奇数個の引数を受け取る関数`makeRoads`を記述します。最初の引数は常に道路の開始点であり、それ以降の引数のペアごとに終了点と距離が指定されます。
¶ `makeRoad`の機能を複製しないでください。`makeRoads`は`makeRoad`を呼び出して実際の道路を作成するようにしてください。
function makeRoads(start) { for (var i = 1; i < arguments.length; i += 2) makeRoad(start, arguments[i], arguments[i + 1]); }
¶ この関数は、`start`という名前付きパラメータを1つ使用し、`arguments`(疑似)配列から他のパラメータを取得します。`i`は、この最初のパラメータをスキップする必要があるため、`1`から開始します。`i += 2`は、覚えているかもしれませんが、`i = i + 2`の省略形です。
var roads = {}; makeRoads("Point Kiukiu", "Hanaiapa", 19, "Mt Feani", 15, "Taaoa", 15); makeRoads("Airport", "Hanaiapa", 6, "Mt Feani", 5, "Atuona", 4, "Mt Ootua", 11); makeRoads("Mt Temetiu", "Mt Feani", 8, "Taaoa", 4); makeRoads("Atuona", "Taaoa", 3, "Hanakee pearl lodge", 1); makeRoads("Cemetery", "Hanakee pearl lodge", 6, "Mt Ootua", 5); makeRoads("Hanapaoa", "Mt Ootua", 3); makeRoads("Puamua", "Mt Ootua", 13, "Point Teohotepapapa", 14); show(roads["Airport"]);
¶ 便利な操作をいくつか定義することで、道路情報の記述を大幅に短縮することができました。語彙を拡張することで、情報をより簡潔に表現したと言えるでしょう。このような「小さな言語」を定義することは、多くの場合非常に強力なテクニックです。— いつでも、反復的または冗長なコードを書いていることに気づいたら、立ち止まって、それをより短く、より密にする語彙を考え出してみてください。
¶ 冗長なコードは書くのが退屈なだけでなく、エラーが発生しやすくなります。考える必要のないことをしているときは、注意が散漫になります。その上、反復コードは変更が困難です。100回繰り返される構造は、それが間違っているか最適ではないことが判明した場合、100回変更する必要があるためです。
¶ 上記のコードをすべて実行した場合、島のすべての道路を含む`roads`という名前の変数があるはずです。特定の場所から始まる道路が必要な場合は、`roads[place]`を実行するだけです。しかし、これらの名前ではあり得ないことではありませんが、地名のタイプミスがあると、期待される配列の代わりに`undefined`が返され、奇妙なエラーが発生します。代わりに、道路配列を取得し、未知の地名を指定すると警告を発する関数を使用します
function roadsFrom(place) { var found = roads[place]; if (found == undefined) throw new Error("No place named '" + place + "' found."); else return found; } show(roadsFrom("Puamua"));
¶ パスファインディングアルゴリズムの最初の試みは、ギャンブラーの方法です
function gamblerPath(from, to) { function randomInteger(below) { return Math.floor(Math.random() * below); } function randomDirection(from) { var options = roadsFrom(from); return options[randomInteger(options.length)].to; } var path = []; while (true) { path.push(from); if (from == to) break; from = randomDirection(from); } return path; } show(gamblerPath("Hanaiapa", "Mt Feani"));
¶ 道路のすべての分岐点で、ギャンブラーはサイコロを振ってどちらの道を行くかを決めます。サイコロが来た道を戻らせたら、そうなります。島のすべての場所は道路でつながっているため、遅かれ早かれ目的地に到着します。
¶ 最も混乱しやすい行は、おそらく`Math.random`を含む行でしょう。この関数は、0から1の間の擬似乱数1を返します。コンソールから数回呼び出してみてください。毎回異なる数値が返される可能性が高くなります。関数`randomInteger`は、この数値に指定された引数を掛け、`Math.floor`で結果を切り捨てます。したがって、たとえば、`randomInteger(3)`は数値`0`、`1`、または`2`を生成します。
¶ ギャンブラーの方法は、構造と計画を嫌悪し、必死に冒険を求める人々のための方法です。ただし、場所間の*最短*ルートを見つけるプログラムを作成しようとしているため、何か他のものが必要になります。
¶ このような問題を解決するための非常に簡単なアプローチは、「生成とテスト」と呼ばれます。それは次のようになります
- 可能なすべてのルートを生成します。
- このセットで、開始点と終了点を実際に接続する最短のルートを見つけます。
¶ ステップ2は難しくありません。ステップ1は少し問題があります。円を含むルートを許可すると、無限の量のルートが存在します。もちろん、円を含むルートは、どこへの最短ルートになる可能性は低く、開始点から始まらないルートも考慮する必要はありません。ヒバオアのような小さなグラフの場合、特定の点から始まるすべての非巡回(円を含まない)ルートを生成できるはずです。
¶ しかし、最初に、いくつかの新しいツールが必要になります。1つ目は`member`という名前の関数で、要素が配列内にあるかどうかを判断するために使用されます。ルートは名前の配列として保持され、新しい場所に到着すると、アルゴリズムは`member`を呼び出して、すでにその場所にいるかどうかを確認します。それは次のようになります
function member(array, value) { var found = false; forEach(array, function(element) { if (element === value) found = true; }); return found; } print(member([6, 7, "Bordeaux"], 7));
¶ ただし、値が最初の位置ですぐに見つかった場合でも、これは配列全体を調べます。なんと無駄なことでしょう。`for`ループを使用する場合、`break`文を使用してループから抜け出すことができますが、`forEach`コンストラクトではこれは機能しません。ループの本体は関数であり、`break`文は関数から抜け出さないためです。1つの解決策は、`forEach`を調整して、特定の種類の例外を中断のシグナルとして認識することです。
var Break = {toString: function() {return "Break";}}; function forEach(array, action) { try { for (var i = 0; i < array.length; i++) action(array[i]); } catch (exception) { if (exception != Break) throw exception; } }
¶ これで、`action`関数が`Break`をスローすると、`forEach`は例外を吸収してループを停止します。変数`Break`に格納されているオブジェクトは、純粋に比較対象として使用されます。`toString`プロパティを与えた唯一の理由は、`forEach`の外部で`Break`例外が発生した場合に、どのような種類の奇妙な値を扱っているのかを理解するのに役立つ可能性があるためです。
¶ `forEach`ループから抜け出す方法があると非常に便利ですが、`member`関数の場合は、結果を明示的に格納して後で返す必要があるため、結果は依然としてかなり醜いです。さらに別の種類の例外`Return`を追加して、`value`プロパティを指定し、そのような例外がスローされたときに`forEach`にこの値を返させることができますが、これは非常に場当たり的で厄介です。私たちが本当に必要なのは、`any`(または`some`と呼ばれることもあります)と呼ばれるまったく新しい高階関数です。それは次のようになります
function any(test, array) { for (var i = 0; i < array.length; i++) { var found = test(array[i]); if (found) return found; } return false; } function member(array, value) { return any(partial(op["==="], value), array); } print(member(["Fear", "Loathing"], "Denial"));
¶ any関数は、配列の要素を左から右へ順に走査し、それぞれにテスト関数を適用します。最初に真値(truthy value)が返された場合、その値を返します。真値が見つからない場合は、falseを返します。 any(test, array)を呼び出すことは、test(array[0]) || test(array[1]) || ... などを行うのとほぼ同じです。
¶ && が || の相棒であるように、any には every という相棒があります。
function every(test, array) { for (var i = 0; i < array.length; i++) { var found = test(array[i]); if (!found) return found; } return true; } show(every(partial(op["!="], 0), [1, 2, -1]));
¶ 必要なもう1つの関数は flatten です。この関数は配列の配列を受け取り、配列の要素を1つの大きな配列にまとめます。
function flatten(arrays) { var result = []; forEach(arrays, function (array) { forEach(array, function (element){result.push(element);}); }); return result; }
¶ concat メソッドと何らかの reduce を使用しても同じことができますが、効率は低下します。文字列を繰り返し連結する方が、配列に入れて join を呼び出すよりも遅いように、配列を繰り返し連結すると、不要な中間配列値が大量に生成されます。
¶ ルートの生成を開始する前に、もう1つ高階関数が必要です。これは filter と呼ばれます。 map と同様に、関数と配列を引数に取り、新しい配列を生成しますが、関数を呼び出した結果を新しい配列に入れる代わりに、指定された関数が真値を返す古い配列の値のみを含む配列を生成します。この関数を記述してください。
function filter(test, array) { var result = []; forEach(array, function (element) { if (test(element)) result.push(element); }); return result; } show(filter(partial(op[">"], 5), [0, 4, 8, 12]));
¶ (filter の適用結果に驚いた場合は、partial に渡された引数は関数の *最初の* 引数として使用されるため、> の左側に配置されることを思い出してください。)
¶ ルートを生成するアルゴリズムがどのように見えるか想像してみてください ― 開始位置から始まり、そこから出ているすべての道路のルートを生成し始めます。これらの道路のそれぞれ終点で、さらにルートを生成し続けます。1つの道路に沿って走るのではなく、枝分かれします。このため、再帰はそれをモデル化する自然な方法です。
function possibleRoutes(from, to) { function findRoutes(route) { function notVisited(road) { return !member(route.places, road.to); } function continueRoute(road) { return findRoutes({places: route.places.concat([road.to]), length: route.length + road.distance}); } var end = route.places[route.places.length - 1]; if (end == to) return [route]; else return flatten(map(continueRoute, filter(notVisited, roadsFrom(end)))); } return findRoutes({places: [from], length: 0}); } show(possibleRoutes("Point Teohotepapapa", "Point Kiukiu").length); show(possibleRoutes("Hanapaoa", "Mt Ootua"));
¶ この関数は、ルートオブジェクトの配列を返します。各ルートオブジェクトには、ルートが通過する場所の配列と長さが含まれています。 findRoutes は再帰的にルートを継続し、そのルートのすべての可能な拡張を含む配列を返します。ルートの終点が目的地である場合、その場所を超えて続行しても意味がないため、そのルートのみを返します。別の場所にいる場合は、続行する必要があります。 flatten/map/filter の行は、おそらく最も読みにくいでしょう。これは、「現在の場所から出ているすべての道路を取得し、このルートが既に訪れた場所に通じる道路を破棄します。これらの道路のそれぞれを続行すると、それぞれに完成したルートの配列が得られるため、これらのすべてのルートを返す1つの大きな配列に入れます。」という意味です。
¶ その行は多くのことを行います。これが、優れた抽象化が役立つ理由です。画面いっぱいのコードを入力することなく、複雑なことを言うことができます。
¶ continueRoute を介して自身を呼び出し続けるため、これは永遠に再帰しませんか?いいえ、ある時点で、すべての発信道路はルートが既に通過した場所に通じるようになり、filter の結果は空の配列になります。空の配列をマップすると空の配列が生成され、それをフラット化しても空の配列が返されます。そのため、行き止まりで findRoutes を呼び出すと空の配列が生成されます。これは、「このルートを続行する方法はありません」を意味します。
¶ 場所は push ではなく concat を使用してルートに追加されることに注意してください。 concat メソッドは新しい配列を作成しますが、push は既存の配列を変更します。関数は単一の部分的なルートから複数のルートに分岐する可能性があるため、複数回使用される必要があるため、元のルートを表す配列を変更してはなりません。
¶ 考えられるすべてのルートがわかったので、最短のルートを見つけましょう。 possibleRoutes と同様に、開始位置と終了位置の名前を引数に取り、shortestRoute という関数を記述します。 possibleRoutes が生成するタイプの単一のルートオブジェクトを返します。
function shortestRoute(from, to) { var currentShortest = null; forEach(possibleRoutes(from, to), function(route) { if (!currentShortest || currentShortest.length > route.length) currentShortest = route; }); return currentShortest; }
¶ 「最小化」または「最大化」アルゴリズムの難しい点は、空の配列が与えられたときに失敗しないことです。この場合、すべての2つの場所の間に少なくとも1つの道路があることがわかっているので、無視することができます。しかし、それは少し物足りないでしょう。プアムアからオオトゥア山への道は急で泥だらけですが、暴風雨によって流されてしまった場合はどうでしょうか?これが原因で関数も壊れてしまうのは残念なので、ルートが見つからない場合は null を返すように注意してください。
¶ 次に、非常に機能的で、すべてを抽象化するアプローチです。
function minimise(func, array) { var minScore = null; var found = null; forEach(array, function(element) { var score = func(element); if (minScore == null || score < minScore) { minScore = score; found = element; } }); return found; } function getProperty(propName) { return function(object) { return object[propName]; }; } function shortestRoute(from, to) { return minimise(getProperty("length"), possibleRoutes(from, to)); }
¶ 残念ながら、他のバージョンの3倍の長さです。複数のものを最小化する必要があるプログラムでは、このような汎用アルゴリズムを記述して再利用できるようにすることをお勧めします。ほとんどの場合、最初のバージョンで十分です。
¶ getProperty 関数に注意してください。オブジェクトで関数型プログラミングを行う場合に役立つことがよくあります。
¶ アルゴリズムがポイントキウキウとポイントテオホテパパパの間でどのようなルートを考え出すか見てみましょう...
show(shortestRoute("Point Kiukiu", "Point Teohotepapapa").places);
¶ ヒバオアのような小さな島では、考えられるすべてのルートを生成するのはそれほど大変な作業ではありません。たとえば、ベルギーのかなり詳細な地図でそれを行おうとすると、途方もない時間がかかります。膨大な量のメモリは言うまでもありません。それでも、オンラインのルートプランナーを見たことがあるでしょう。これらは、ほんの数秒で巨大な道路の迷宮を通り抜ける、ほぼ最適なルートを提供します。彼らはどのようにそれを行うのでしょうか?
¶ 注意を払っていれば、すべてのルートを最後まで生成する必要がないことに気づいたかもしれません。ルートを構築 *しながら* 比較を開始すると、この大きなルートセットの構築を回避でき、目的地への単一のルートが見つかったらすぐに、そのルートよりも既に長いルートの拡張を停止できます。
¶ これを試すために、20 x 20のグリッドをマップとして使用します。

¶ ここで見ているのは、山岳地帯の標高マップです。黄色の点は山頂、青色の点は谷です。この地域は、100メートルの正方形に分割されています。 x と y プロパティを持つオブジェクトによって正方形が表される場合、そのマップ上の任意の正方形の高さをメートル単位で示すことができる heightAt という関数を利用できます。
print(heightAt({x: 0, y: 0})); print(heightAt({x: 11, y: 18}));
¶ 私たちは、徒歩で、左上から右下まで、この風景を横断したいと考えています。グリッドはグラフのように扱うことができます。すべての正方形はノードであり、周囲の正方形に接続されています。
¶ 私たちはエネルギーを無駄にしたくないので、できるだけ簡単なルートを選びたいと思っています。上り坂は下り坂よりも重く、下り坂は水平よりも重いです2。この関数は、隣接する2つの正方形間の「加重メートル」の量を計算します。これは、それらの間を歩いたり登ったりすることでどれだけ疲れるかを表しています。上り坂は下り坂の2倍の重さとして数えられます。
function weightedDistance(pointA, pointB) { var heightDifference = heightAt(pointB) - heightAt(pointA); var climbFactor = (heightDifference < 0 ? 1 : 2); var flatDistance = (pointA.x == pointB.x || pointA.y == pointB.y ? 100 : 141); return flatDistance + climbFactor * Math.abs(heightDifference); }
¶ flatDistance の計算に注意してください。2つの点が同じ行または列にある場合、それらはすぐ隣にあり、それらの間の距離は100メートルです。そうでない場合、それらは斜めに隣接していると見なされ、このサイズの2つの正方形間の斜め距離は2の平方根の100倍、つまり約 141 になります。1ステップ以上離れた正方形に対してこの関数を呼び出すことはできません。(ダブルチェックできますが...めんどくさいです。)
¶ マップ上のポイントは、x および y プロパティを含むオブジェクトによって表されます。これらの3つの関数は、そのようなオブジェクトを操作するときに役立ちます。
function point(x, y) { return {x: x, y: y}; } function addPoints(a, b) { return point(a.x + b.x, a.y + b.y); } function samePoint(a, b) { return a.x == b.x && a.y == b.y; } show(samePoint(addPoints(point(10, 10), point(4, -2)), point(14, 8)));
¶ このマップを介したルートを見つける場合は、再び「道標」、つまり指定されたポイントから取ることができる方向のリストを作成する関数が必要になります。ポイントオブジェクトを引数に取り、近くのポイントの配列を返す possibleDirections 関数を記述します。直線と斜めの両方で隣接するポイントにのみ移動できるため、正方形には最大8つの隣接点があります。マップの外側にある正方形を返さないように注意してください。私たちが知っている限り、マップの端は世界の端かもしれません。
function possibleDirections(from) { var mapSize = 20; function insideMap(point) { return point.x >= 0 && point.x < mapSize && point.y >= 0 && point.y < mapSize; } var directions = [point(-1, 0), point(1, 0), point(0, -1), point(0, 1), point(-1, -1), point(-1, 1), point(1, 1), point(1, -1)]; return filter(insideMap, map(partial(addPoints, from), directions)); } show(possibleDirections(point(0, 0)));
¶ 20 を2回書かなくても済むように、mapSize という変数を作成しました。いつか、別のマップに同じ関数を使用したい場合、コードが 20 でいっぱいで、すべて変更する必要がある場合、扱いにくくなります。 mapSize を possibleDirections の引数にすることさえできます。そのため、関数を変更することなく、異なるマップに使用できます。ただし、この場合は必要ないと判断しました。そのようなことは、必要が生じたときにいつでも変更できます。
¶ では、なぜ2回出現する 0 を保持する変数も追加しなかったのでしょうか?マップは常に 0 から始まると思い込んでいたので、これは変更される可能性が低く、変数を使用してもノイズが増えるだけです。
¶ ブラウザが終了するのに時間がかかりすぎるためにプログラムが中断されることなく、このマップ上のルートを見つけるには、アマチュアの試みを中止し、本格的なアルゴリズムを実装する必要があります。過去には、このような問題に多くの労力が費やされ、多くのソリューションが設計されてきました(素晴らしいものもあれば、役に立たないものもあります)。非常に人気があり効率的なものの1つは、A *(Aスターと発音)と呼ばれます。章の残りの部分では、マップのA *ルート検索関数を実装します。
¶ アルゴリズム自体に入る前に、それが解決する問題についてもう少し説明しましょう。グラフを通して経路を検索する際の問題は、大きなグラフには非常に多くの経路が存在することです。Hiva Oaの経路探索プログラムは、グラフが小さい場合は、経路が既に通過した点を再訪しないようにするだけで十分であることを示しました。しかし、新しい地図では、これだけでは不十分です。
¶ 根本的な問題は、間違った方向に進む余地が多すぎることです。目標に向かって経路の探索を誘導する何らかの方法がない限り、与えられた経路を続けるための選択は、正しい方向よりも間違った方向に進む可能性が高くなります。そのような方法で経路を生成し続けると、膨大な量の経路が生成され、その中の1つが偶然終点に到達したとしても、それが最短経路であるかどうかは分かりません。
¶ そのため、終点に到達する可能性の高い方向を最初に探索する必要があります。私たちの地図のようなグリッドでは、経路の長さと終点が終点にどれだけ近いかを確認することで、経路の良し悪しを大まかに推定できます。経路の長さと、まだ進む必要がある距離の推定値を加算することで、どの経路が有望かを大まかに把握できます。有望な経路を最初に拡張すれば、無駄な経路に時間を浪費する可能性が低くなります。
¶ しかし、それでもまだ十分ではありません。地図が完全に平坦な平面であれば、有望に見える経路はほぼ常に最良の経路となり、上記の módszer を使用して目標まで直接進むことができます。しかし、私たちの経路には谷や丘陵地帯が障害物として存在するため、どの向きが最も効率的な経路になるかを事前に判断することは困難です。このため、依然として探索しなければならない経路が多すぎます。
¶ これを修正するために、最も有望な経路を常に最初に探索しているという事実を巧みに利用することができます。経路Aが点Xに到達するための最良の方法であると判断したら、それを記憶することができます。後で、経路Bも点Xに到達した場合、それが最良の経路ではないことが分かっているので、それ以上探索する必要はありません。これは、プログラムが多くの無意味な経路を構築するのを防ぐことができます。
¶ アルゴリズムは、次のようなものです...
¶ 追跡すべきデータは2つあります。1つ目はオープンリストと呼ばれ、まだ探索する必要がある部分的な経路が含まれています。各経路にはスコアがあり、その長さと目標からの推定距離を加算することで計算されます。この推定値は常に楽観的でなければならず、距離を過大評価してはなりません。2つ目は、私たちが確認したノードの集合と、そこに到達した最短の部分経路です。これを到達リストと呼びます。最初に、開始ノードのみを含む経路をオープンリストに追加し、到達リストに記録します。
¶ 次に、オープンリストにノードがある限り、スコアが最も低い(最良の)ノードを取り出し、それをどのように続けることができるかを見つけます(`possibleDirections`を呼び出すことによって)。これが返す各ノードについて、元の経路にそれを追加し、`weightedDistance`を使用して経路の長さを調整することにより、新しい経路を作成します。これらの新しい経路のそれぞれの終点は、到達リストで検索されます。
¶ ノードがまだ到達リストにない場合、それはまだ見ていないことを意味し、新しい経路をオープンリストに追加し、到達リストに記録します。以前に見たことがある場合は、新しい経路のスコアと到達リストにある経路のスコアを比較します。新しい経路の方が短い場合は、既存の経路を新しい経路に置き換えます。そうでない場合は、そのポイントに到達するためのより良い方法を既に見ているため、新しい経路を破棄します。
¶ オープンリストから取得した経路がゴールノードで終わるまで、これを続けます。その場合、経路が見つかったことになります。または、オープンリストが空になるまで、これを続けます。その場合、経路がないことが分かります。私たちの場合、地図には乗り越えられない障害物はないため、常に経路が存在します。
¶ オープンリストから取得した最初の完全な経路が最短経路でもあると、どのようにして分かるのでしょうか?これは、スコアが最も低い経路のみを検討するという事実の結果です。経路のスコアは、実際の長さと残りの長さの*楽観的な*推定値です。これは、経路がオープンリストで最も低いスコアを持っている場合、それは常にその現在の終点への最良の経路であることを意味します。別の経路が後でそのポイントへのより良い方法を見つけることは不可能です。なぜなら、もしそれがより良いものであれば、そのスコアはより低かったはずだからです。
¶ なぜこれがうまくいくのかという細かい点がまだ理解できていない場合でも、イライラしないでください。このようなアルゴリズムについて考えるとき、「似たようなもの」を以前に見たことがあると、そのアプローチを比較するための基準点ができるため、非常に役立ちます。初心者のプログラマーは、そのような基準点なしで作業する必要があるため、迷子になりがちです。これは高度な内容であることを理解し、残りの章をざっと読んで、挑戦したいと思ったときに改めて戻ってきてください。
¶ 残念ながら、アルゴリズムのある側面については、再び魔法を使う必要があります。オープンリストは、大量の経路を保持し、その中で最もスコアが低い経路をすばやく見つけることができなければなりません。通常の配列に格納し、毎回この配列を検索するのは、非常に遅いため、バイナリヒープと呼ばれるデータ構造を提供します。`Date`オブジェクトと同様に、`new`を使用して作成し、その要素を「スコアリング」するために使用される関数を引数として渡します。結果のオブジェクトには、配列と同様に`push`メソッドと`pop`メソッドがありますが、`pop`は、最後に`push`された要素ではなく、常にスコアが最も低い要素を返します。
function identity(x) { return x; } var heap = new BinaryHeap(identity); forEach([2, 4, 5, 1, 6, 3], function(number) { heap.push(number); }); while (heap.size() > 0) show(heap.pop());
¶ 付録2では、このデータ構造の実装について説明しています。これは非常に興味深いものです。第8章を読んだ後、見てみるのも良いでしょう。
¶ 可能な限り効率を上げる必要があるということは、別の影響を及ぼします。Hiva Oaアルゴリズムは、場所の配列を使用して経路を格納し、`concat`メソッドを使用して経路を拡張するときにそれらをコピーしました。今回は、非常に多くの経路を探索するため、配列をコピーする余裕はありません。代わりに、オブジェクトの「チェーン」を使用して経路を格納します。チェーン内のすべてのオブジェクトには、地図上の点やこれまでの経路の長さなどのプロパティがあり、チェーン内の前のオブジェクトを指すプロパティもあります。以下のようになります。
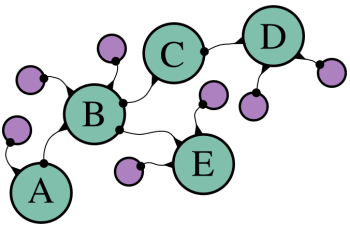
¶ ここで、シアン色の円は関連するオブジェクトであり、線はプロパティを表しています。ドットが付いた端はプロパティの値を指しています。オブジェクト`A`はここでの経路の開始点です。オブジェクト`B`は、`A`から続く新しい経路を構築するために使用されます。`from`と呼ぶプロパティがあり、それが基づいている経路を指しています。後で経路を再構築する必要がある場合は、これらのプロパティをたどって、経路が通過したすべての点を見つけることができます。オブジェクト`B`は2つの経路の一部であり、1つは`D`で終わり、もう1つは`E`で終わることに注意してください。経路が多い場合、これは多くの 저장 용량 を節約できます。新しい経路ごとに、それ自体のための新しいオブジェクトが1つだけ必要であり、残りは同じように開始された他の経路と共有されます。
¶ 2点間の距離の楽観的な推定値を与える`estimatedDistance`関数を作成してください。高さデータを考慮する必要はなく、平坦な地図を想定できます。直線と斜め方向にのみ移動し、2つの正方形間の斜め距離を`141`と数えていることに注意してください。
function estimatedDistance(pointA, pointB) { var dx = Math.abs(pointA.x - pointB.x), dy = Math.abs(pointA.y - pointB.y); if (dx > dy) return (dx - dy) * 100 + dy * 141; else return (dy - dx) * 100 + dx * 141; }
¶ 奇妙な公式は、経路を直線部分と斜め部分に分解するために使用されます。次のような経路がある場合...
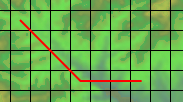
¶ ...経路の幅は`6`マス、高さは`3`マスなので、`6 - 3 = 3`回の直線移動と`3`回の斜め移動になります。
¶ 2点間の直線の「ピタゴラスの」距離を計算するだけの関数を作成した場合でも、それは機能します。必要なのは楽観的な推定値であり、目標に直接行けると仮定するのは確かに楽観的です。ただし、推定値が実際の距離に近いほど、プログラムが試してみる必要のある無駄な経路は少なくなります。
¶ オープンリストにはバイナリヒープを使用します。到達リストにはどのようなデータ構造が適しているでしょうか?これは、`x`、`y`座標のペアが与えられた場合に、経路を検索するために使用されます。できれば高速な方法で。`makeReachedList`、`storeReached`、`findReached`の3つの関数を作成してください。最初の関数はデータ構造を作成し、2番目の関数は、到達リスト、点、および経路が与えられた場合に、経路を格納し、最後の関数は、到達リストと点が与えられた場合に、経路を取得するか、経路が見つからないことを示すために`undefined`を返します。
¶ 1つの合理的なアイデアは、オブジェクト内にオブジェクトを持つオブジェクトを使用することです。点の座標の1つ、たとえば`x`を、外側のオブジェクトのプロパティ名として使用し、もう1つの座標`y`を内側のオブジェクトのプロパティ名として使用します。これには、探している内側のオブジェクトが(まだ)存在しない場合があるという事実を処理するためにある程度のブックキーピングが必要です。
function makeReachedList() { return {}; } function storeReached(list, point, route) { var inner = list[point.x]; if (inner == undefined) { inner = {}; list[point.x] = inner; } inner[point.y] = route; } function findReached(list, point) { var inner = list[point.x]; if (inner == undefined) return undefined; else return inner[point.y]; }
¶ 別の可能性は、点の`x`と`y`を単一のプロパティ名にマージし、それを使用して単一のオブジェクトに経路を格納することです。
function pointID(point) { return point.x + "-" + point.y; } function makeReachedList() { return {}; } function storeReached(list, point, route) { list[pointID(point)] = route; } function findReached(list, point) { return list[pointID(point)]; }
¶ データ構造を作成および操作するための一連の関数を提 供することにより、データ構造のタイプを定義することは有用な手法です。これにより、構造を利用するコードを、構造自体の詳細から「分離」することができます。上記の2つの実装のどちらを使用しても、到達リストを必要とするコードはまったく同じように動作することに注意してください。期待どおりの結果が得られる限り、どのような種類のオブジェクトが使用されているかは関係ありません。
¶ これは第8章でさらに詳細に議論されます。そこでは、newを使用して作成され、操作するためのメソッドを持つBinaryHeapのようなオブジェクト型を作成する方法を学びます。
¶ ここでようやく実際の経路探索関数を確認します。
function findRoute(from, to) { var open = new BinaryHeap(routeScore); var reached = makeReachedList(); function routeScore(route) { if (route.score == undefined) route.score = estimatedDistance(route.point, to) + route.length; return route.score; } function addOpenRoute(route) { open.push(route); storeReached(reached, route.point, route); } addOpenRoute({point: from, length: 0}); while (open.size() > 0) { var route = open.pop(); if (samePoint(route.point, to)) return route; forEach(possibleDirections(route.point), function(direction) { var known = findReached(reached, direction); var newLength = route.length + weightedDistance(route.point, direction); if (!known || known.length > newLength){ if (known) open.remove(known); addOpenRoute({point: direction, from: route, length: newLength}); } }); } return null; }
¶ まず、必要なデータ構造、つまりオープンリストと到達済みリストを1つずつ作成します。 routeScoreは、バイナリヒープに与えられるスコアリング関数です。複数回再計算するのを避けるために、結果がルートオブジェクトにどのように格納されるかに注目してください。
¶ addOpenRouteは、新しいルートをオープンリストと到達済みリストの両方に追加する便利な関数です。これは、ルートの開始を追加するためにすぐに使用されます。ルートオブジェクトには常に、ルートの終点となるポイントを保持するpointプロパティと、ルートの現在の長さを保持するlengthプロパティがあります。複数のマスにわたるルートには、先行ルートを指すfromプロパティもあります。
¶ アルゴリズムで説明したように、whileループはオープンリストから最もスコアが低いルートを取り続け、それが目標地点に到達するかどうかを確認します。到達しない場合は、それを拡張することで続行する必要があります。これはforEachが処理するものです。新しいポイントを到達済みリストで検索します。そこに見つからない場合、または見つかったノードの長さが新しいルートよりも長い場合は、新しいルートオブジェクトが作成されてオープンリストと到達済みリストに追加され、既存のルート(存在する場合)はオープンリストから削除されます。
¶ known内のルートがオープンリストにない場合はどうでしょうか?ルートは、終点への最適なルートであることが判明した場合にのみオープンリストから削除されるため、必ず存在するはずです。バイナリヒープに存在しない値を削除しようとすると、例外がスローされます。そのため、私の推論が間違っている場合、関数を実行すると例外が発生する可能性があります。
¶ コードが複雑になりすぎて、特定のことに疑問を抱くようになった場合は、何か問題が発生したときに例外を発生させるチェックを追加することをお勧めします。そうすれば、「静かに」奇妙なことが起こっていないことがわかり、何かを壊したときに、すぐに何が壊れたかがわかります。
¶ このアルゴリズムは再帰を使用していませんが、それでもすべての分岐を探索できます。オープンリストは、関数呼び出しスタックがHiva Oa問題の再帰的解決策で果たした役割を多かれ少なかれ引き継ぎます。つまり、まだ探索する必要があるパスを追跡します。「まだ実行する必要があること」を格納するデータ構造を使用することにより、すべての再帰アルゴリズムを非再帰的な方法で書き直すことができます。
¶ それでは、経路探索を試してみましょう。
var route = findRoute(point(0, 0), point(19, 19));
¶ 上記のすべてのコードを実行し、エラーが発生しなかった場合、その呼び出しは実行に数秒かかる場合がありますが、ルートオブジェクトが返されます。このオブジェクトは、かなり読みにくいです。コンソールが十分に大きい場合、マップ上にルートを表示するshowRoute関数を使用すると、読みやすくなります。
showRoute(route);
¶ showRouteに複数のルートを渡すこともできます。これは、たとえば、美しい視点11、17を含む景観ルートを計画しようとしている場合に役立ちます。
showRoute(findRoute(point(0, 0), point(11, 17)), findRoute(point(11, 17), point(19, 19)));
¶ グラフを通る最適なルートを検索するというテーマのバリエーションは、多くの問題に適用できます。その多くは、物理的なパスを見つけることとはまったく関係ありません。たとえば、限られたスペースに複数のブロックを配置するパズルを解く必要があるプログラムは、特定のブロックを特定の場所に配置しようとすることで得られるさまざまな「パス」を探索することで、これを行うことができます。最後のブロックのためのスペースが不足しているパスは行き止まりであり、すべてのブロックを収めることができたパスが解決策です。